Your personal knowledge is your most valuable asset

Connecting and discussing knowledge
LDC is a well thought-out tool for organizing your knowledge. Note down your new ideas quickly and easily and put them into a larger context. LDC helps you to create, manage and share your notes with colleagues. It enables you to visualize and discuss complex relationships in a completely new and transparent way
Create cards
LDC is organised in cards (this is equivalent to notes). You can create as many as you want. You can fill them with information and link them with other cards and outside sources.
Cards can contain text and be enriched with images and diagrams. They can be linked to other cards as well.


Link cards
Cards can be arranged in hierarchies and nets. Superordinated cards are shown in the top-left corner. In the top-right corner you see which cards have direct, non-hierarchical associations.
Powerful search
What is the purpose of writing notes if you cannot find them? We know your pain. We integrated a powerful search to find what you are looking for.
You can filter the cards by user, collection or a powerful full text search. Our goal is to make it as easy as possible to find the cards you are looking for.

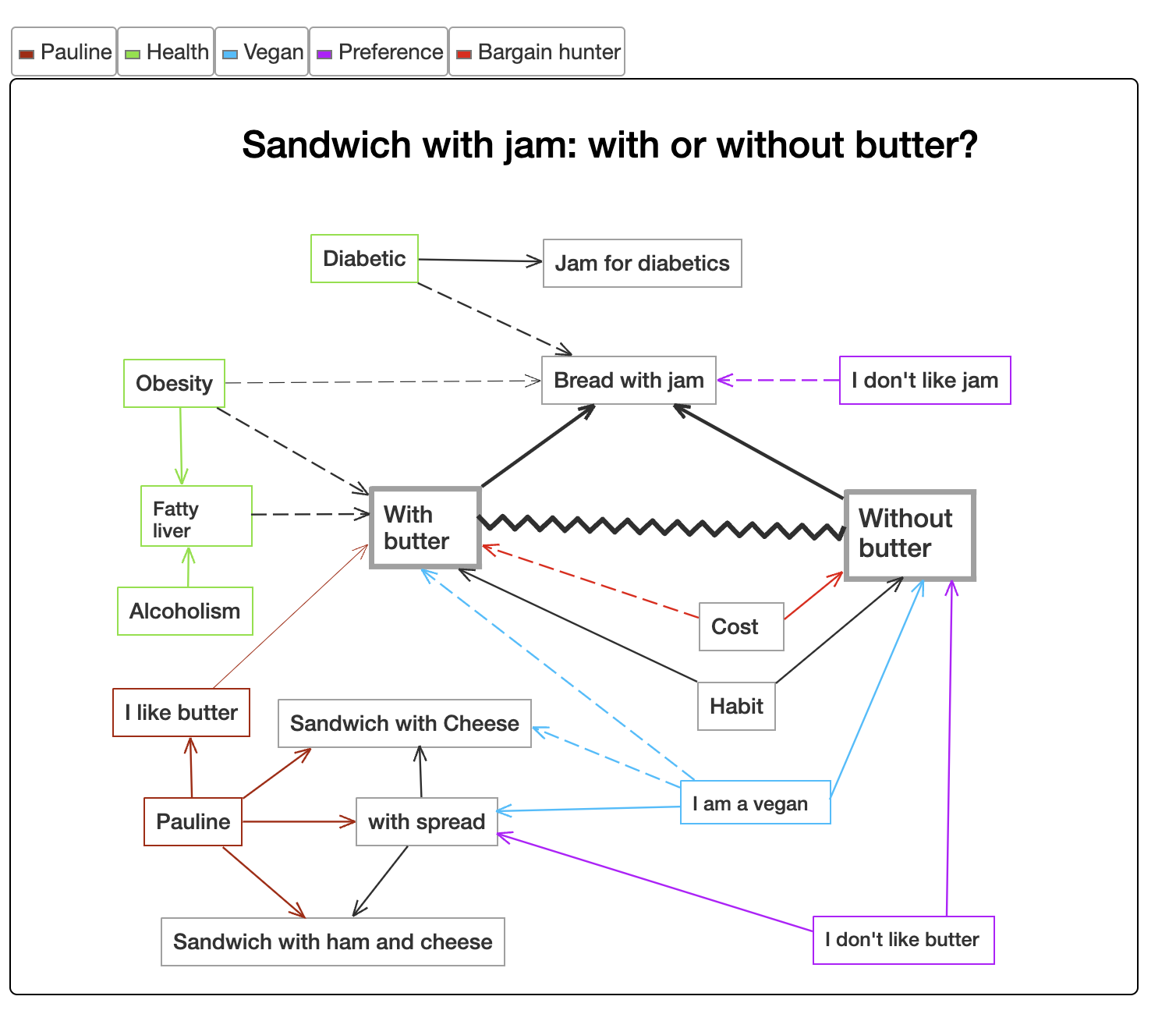
Views
Views are built by a novel argument editor and form the core of LDC. They expand the digital Zettelkasten into a refined tool for discussion and logic.
What are Views good for? The views allow you to combine arguments and keywords, summarise different opinions and explore their detailed front lines. Note contradictions, strengthenings and weakenings between the arguments, place explaining cards behind the individual keywords of the views and create your own integral and transparent network of arguments for your work and for open discussions.
The multiuser system of LDC is built for just that!

Are you interested?
Then click the button below to get instant access to an immediate free trial!





